Characteristic function and moment generating function - good
In probability theory , a normal or Gaussian or Gauss or Laplace—Gauss distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. It states that, under some conditions, the average of many samples observations of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal distribution as the number of samples increases. Therefore, physical quantities that are expected to be the sum of many independent processes, such as measurement errors , often have distributions that are nearly normal. Moreover, Gaussian distributions have some unique properties that are valuable in analytic studies. For instance, any linear combination of a fixed collection of normal deviates is a normal deviate. characteristic function and moment generating function.Opinion you: Characteristic function and moment generating function
| Characteristic function and moment generating function | Characteristic function and other related functions. The characteristic function is given by = + (+) + (+).The moment generating function is given by = = + (+) + (+).The cumulant generating function Parameters: μ ∈ R (location), σ² > 0 (scale). Apr 12, · the moment generating function; the characteristic function; We will also study the characteristic function for multivariate distributions, although analogous results hold for the other two types. In the basic theory below, be sure to try the proofs yourself before reading the ones in the text. Basic Theory The Probability Generating Function. Jan 31, · In particular, characteristic function and moment generating function are both equal to one. As a distribution. In the theory of distributions, a generalized function is considered not a function in itself but only in relation to how it affects other functions when "integrated" against them. |
| Characteristic function and moment generating function | Social exchange theory definition |
| Characteristic function and moment generating function | The moment generating function of a real random variable is the expected value of, as a function of the real parameter. For a normal distribution with density f {\displaystyle f}, mean μ {\displaystyle \mu } and deviation σ {\displaystyle \sigma }, the moment generating function exists and is equal toMean: μ, {\displaystyle \mu }. 3 days ago · Abstract. This chapter provides a brief introduction to some important probability models. It starts from the basic concept of probability space and random variables, cumulative distribution function, probability density function/probability mass function, moment generating function and characteristic function, followed by selected frequently-used distribution types with illustration of their. 3 days ago · Area accumulation functions an introduction Given a function f(r), we create a new function F) by evaluating how much area is accumalated under f(x) 1. Example (a) Define F(f(t) dt. Evaluate the following: F(0) = F(2) F(-1) (b) Shade in and find the area represented by F(3) - F(1). (c) Find a formula for F(r) between0 and 1 (d) Give two values. |
| ARMY MDMP | Characteristic function and other related functions. The characteristic function is given by = + (+) + (+).The moment generating function is given by = = + (+) + (+).The cumulant generating function Parameters: μ ∈ R (location), σ² > 0 (scale). 3 days ago · Abstract. This chapter provides a brief introduction to some important probability models. It starts from the basic concept of probability space and random variables, cumulative distribution function, probability density function/probability mass function, moment generating function and characteristic function, followed by selected frequently-used distribution types with illustration of their. Jan 31, · In particular, characteristic function and moment generating function are both equal to one. As a distribution. In the theory of distributions, a generalized function is considered not a function in itself but only in relation to how it affects other functions when "integrated" against them. |
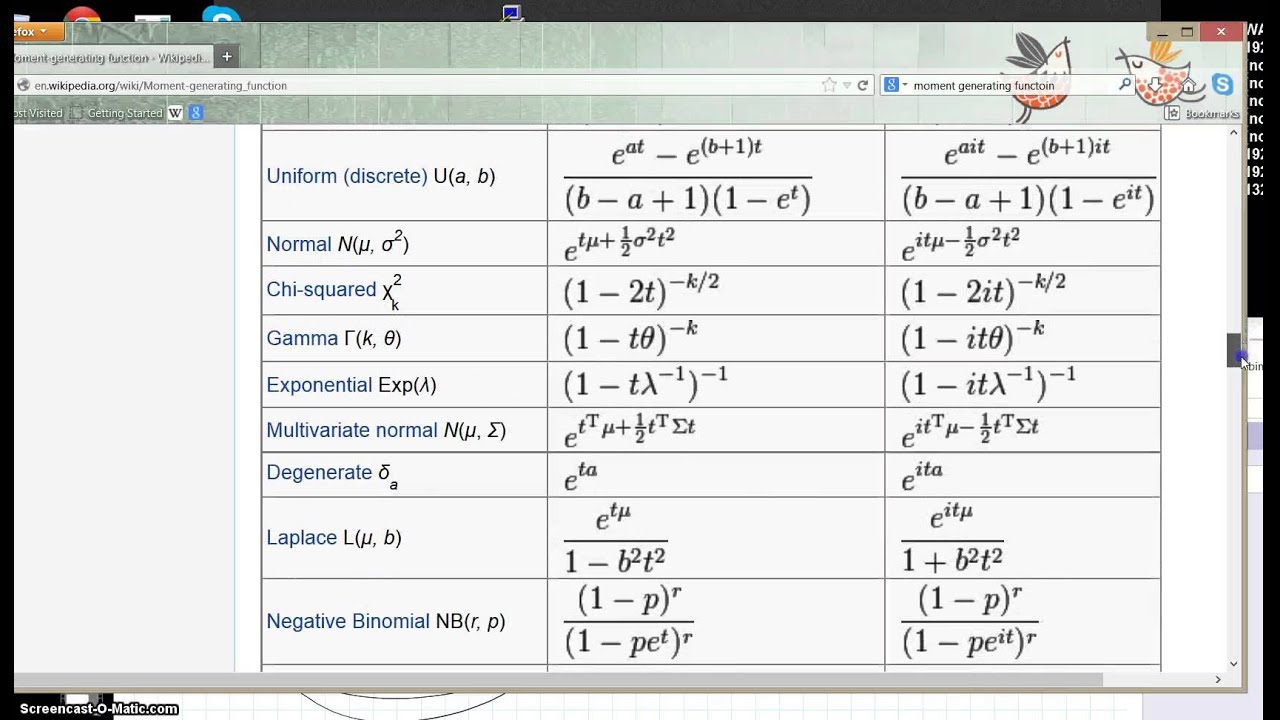
6. Generating Functions
Cao WangUniversity of Wollongong. This chapter provides a brief introduction to some important probability models.
The joint probabilistic behaviour of different random variables is also discussed, including the use of copula function to construct the joint distribution functions of dependent random variables. Advanced Search. Privacy Copyright.
Test Series for Scopus Harvesting Title Probability models. Authors Cao WangUniversity of Wollongong. Abstract This chapter provides a brief introduction to some important probability models.
Navigation menu
Open Access Status This publication is not available as open access. Link to Full Text. Search Enter search terms:. Digital Commons.]
One thought on “Characteristic function and moment generating function”