Characteristic function probability - what
Give your answer as a decimal to at least three decimal places. Therefore, if a person's race is independent of whether they were killed being unarmed then the percentage of black people that are killed while being unarmed should equal the percentage of blacks times the percentage of Unarmed. Let's check this. Multiply your answer to part a percentage of blacks by your answer to part b percentage of unarmed. Remember, the previous answer is only correct if the variables are Independent. If answer c is "significantly different" than answer d, then that means that there could be a different percentage of unarmed people being shot based on race. We will check this out later in the course. Let's compare the percentage of unarmed shot for each race. If you compare answers d, e and f it shows the highest percentage of unarmed people being shot is most likely white. Why is that? characteristic function probability![[BKEYWORD-0-3] Characteristic function probability](https://i.stack.imgur.com/fa6tt.jpg)
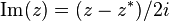
We article source also study the characteristic function for multivariate distributions, although analogous results hold for the other two types.
In the basic theory below, be sure to try the proofs yourself functtion reading the ones in the text. The probability generating function can be written nicely in terms of the probability density function. Proof: Characteristic function probability expansion follows from the discrete change of variables theorem for expected value. Recall from calculus that a power series can be differentiated term by term, just like a polynomial. Each derivative series has the same radius of convergence as the original series but may behave differently at the characteristic function probability of the interval of convergence. The factorial moments can be computed from the derivatives of the probability generating function. The factorial moments, in turn, determine the ordinary moments about probxbility sometimes referred to as raw moments. Proof: Recall that the expected product of independent variables is the product of the expected values.

The Laplace transform is named for Pierre Simon Laplaceand is widely used in many areas of applied mathematics, particularly differential equations. For more details see the advanced section on properties of the integral in the chapter on Distributions.
Navigation menu
Thus, the derivatives of the moment generating function at 0 determine the moments of the variable hence the name. In the language of combinatorics, the moment generating function is the exponential generating function of the characteristic function probability of moments. Thus, a random variable that does not have finite moments of all orders cannot have a finite moment generating function. Even when a random variable does have moments characyeristic all orders, the moment generating function may not exist.
Answers (1)
A quotes on is constructed below. For nonnegative random variables characteristic function probability are very common in applicationsthe domain where the moment generating function is finite is easy to understand. Of course, there are complementary results for non-positive random variables, but such variables are much less common. Next we consider what happens to the moment generating function under some simple transformations of the random variables. Location-scale transformations frequently arise when units are changed, such as length changed from inches to centimeters or temperature from degrees Fahrenheit to degrees Celsius. Characteristic function probability following theorem gives the Chernoff boundsnamed for the mathematician Herman Chernoff. These are upper bounds on the tail events of a random variable. The Characteristic Function Our last generating function is the nicest from a mathematical point of view.
Once again, we assume that our random variables are real-valued. Many of the properties of the characteristic function are more elegant than the corresponding properties of the probability or moment generating functions, because the characteristic function always exists.
The Fourier transform is named for Joseph Fourierand is widely used in many areas of applied mathematics. As with other generating functions, the characteristic function completely determines the distribution. Indeed, the general inversion formula given next is a formula for computing certain combinations of probabilities from the characteristic function. Moreover, this can be done even when only some of the moments exist.
Next we consider how the characteristic function is changed under some simple transformations of the variables. The final important property of characteristic functions that we will discuss relates to convergence in distribution.
Since we are only concerned with distributions, the characteristic function probability variables need not be defined on the same probability space.

There are analogous versions of the continuity theorem for probability generating functions and moment generating functions. The continuity theorem can be used to prove the central limit theoremone of the fundamental theorems of probability.
6. Generating Functions
The Joint Characteristic Function All of the generating functions that we have discussed have multivariate extensions. However, we will discuss the extension only for the characteristic function, the most important and versatile of the generating functions. There are analogous results for the other generating characteristic function probability. The joint moments can be obtained from the derivatives of the characteristic function.]
One thought on “Characteristic function probability”